
《平面向量的应用》平面向量及其应用PPT下载(第二课时正弦定理)
第一部分内容:内容标准
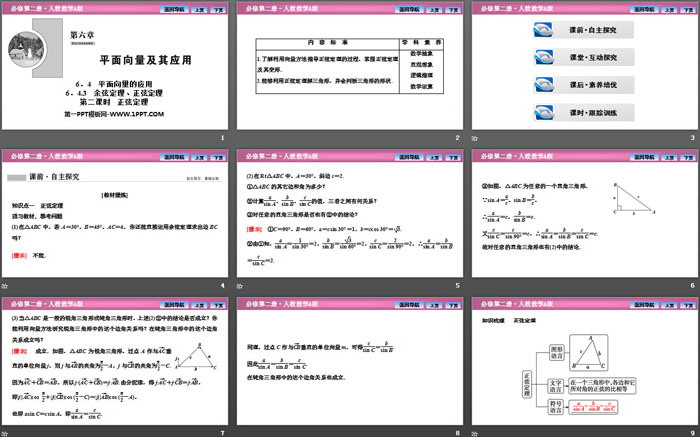
1.了解利用向量方法推导正弦定理的过程,掌握正弦定理及其变形.
2.能够利用正弦定理解三角形,并会判断三角形的形状.
... ... ...
平面向量的应用PPT,第二部分内容:课前 • 自主探究
[教材提炼]
知识点一 正弦定理
预习教材,思考问题
(1)在△ABC中,若A=30°,B=45°,AC=4,你还能直接运用余弦定理求出边BC吗?
(2)在Rt△ABC中,A=30°,斜边c=2.
①△ABC的其它边和角为多少?
②计算asin A,bsin B,csin C的值,三者之间有何关系?
③对任意的直角三角形是否也有②中的结论?
(3)当△ABC是一般的锐角三角形或钝角三角形时,上述(2)②中的结论是否成立?你能利用向量方法研究锐角三角形中的这个边角关系吗?在钝角三角形中的这个边角关系成立吗?
知识点二 正弦定理的推论
预习教材,思考问题
在正弦定理中,三角形的各边与其所对角的正弦的比都相等,那么这个比值与该三角形外接圆的直径有什么关系?
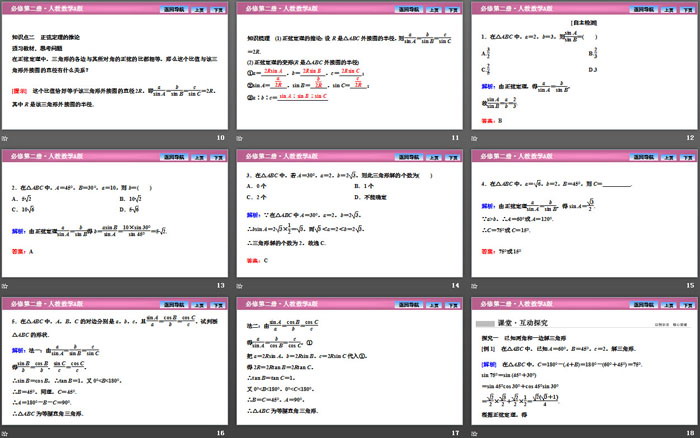
知识梳理 (1)正弦定理的推论:设R是△ABC外接圆的半径,则asin A=bsin B=csin C=2R.
(2)正弦定理的变形(R是△ABC外接圆的半径)
①a=________,b=________,c=________;
②sin A=________,sin B=________,sin C=________;
③a∶b∶c=________
... ... ...
平面向量的应用PPT,第三部分内容:课堂 • 互动探究
探究一 已知两角和一边解三角形
[例1] 在△ABC中,已知A=60°,B=45°,c=2,解三角形.
方法提升
解决已知两角及一边类型的解题方法
(1)若所给边是已知角的对边时,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
探究二 已知两边和其中一边的对角解三角形
[例2] 在△ABC中,根据下列条件,解三角形.
(1)A=60°,c=2,a=6;
(2)a=3,b=2,B=45°.
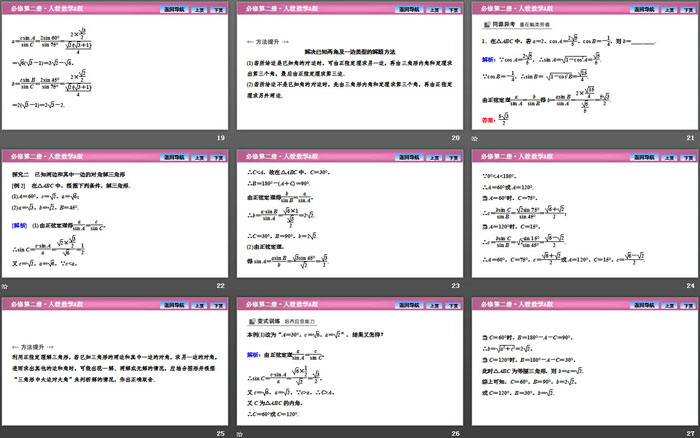
方法提升
利用正弦定理解三角形,若已知三角形的两边和其中一边的对角,求另一边的对角,进而求出其他的边和角时,可能出现一解、两解或无解的情况,应结合图形并根据“三角形中大边对大角”来判断解的情况,作出正确取舍.
探究三 判断三角形的形状
[例3] 在△ABC中,角A、B、C的对边分别为a、b、c,若b=acos C,试判定△ABC的形状.
方法提升
1.判断三角形形状时,应围绕三角形的边角关系,利用正弦或余弦定理进行边角互化,要么把角转化为边,通过代数变形找出边之间的关系,要么把边转化为角,通过三角变换找出角之间的关系,当然也可以边角同时考虑.
2.在解题中,若出现关于边的齐次式(方程),或关于角的正弦的齐次式(方程)可通过正弦定理,进行边角互化.
... ... ...
平面向量的应用PPT,第四部分内容:课后 • 素养培优
一、“剪不断,理还乱”——忽略大边对大角致错
直观想象、逻辑推理、数学运算
[典例1] 在△ABC中,已知a=23,b=2,A=60°,则B=__________.
[素养提升] 在同一三角形中,大边对大角,反过来,大角对大边,由此,在利用正弦定理解三角形时,要对三角形解的个数进行判断,防止产生增根.
二、火眼金睛识别三角形解的情况
直观想象、逻辑推理、数学运算
在△ABC中,已知a,b和A时,解的情况
[典例2] 在△ABC中,已知a=23,b=6,A=30°,求B、C和c.
关键词:高中人教A版数学必修二PPT课件免费下载,平面向量的应用PPT下载,平面向量及其应用PPT下载,正弦定理PPT下载,.PPT格式;
更多关于《 平面向量及其应用 平面向量的应用 正弦定理 》PPT课件, 请点击 平面向量及其应用PPT平面向量的应用PPT正弦定理PPT标签。
《平面向量的应用》平面向量及其应用PPT下载(第四课时余弦定理、正弦定理应用举例):
《平面向量的应用》平面向量及其应用PPT下载(第四课时余弦定理、正弦定理应用举例) 第一部分内容:内容标准 1.了解实际测量中专用名词与术语. 2.熟练掌握正、余弦定理. 3.能用余弦..
《平面向量的应用》平面向量及其应用PPT下载(第三课时正弦定理和余弦定理的综合应用):
《平面向量的应用》平面向量及其应用PPT下载(第三课时正弦定理和余弦定理的综合应用) 第一部分内容:内容标准 1.掌握三角形的面积公式及其应用. 2.熟练掌握利用正、余弦定理判断三角..
《平面向量的应用》平面向量及其应用PPT下载(第一课时余弦定理):
《平面向量的应用》平面向量及其应用PPT下载(第一课时余弦定理) 第一部分内容:内容标准 1.会借助向量的运算,探索三角形边长与角度的关系. 2.掌握余弦定理及其推论. 3.能够利用余..