《三角恒等变换》三角函数PPT课件(第2课时两角和与差的正弦、余弦公式)
第一部分内容:学 习 目 标
1.掌握两角差的余弦公式推导出两角和的余弦公式及两角和与差的正弦公式.
2.会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简、计算等.
3.熟悉两角和与差的正弦、余弦公式的灵活运用,了解公式的正用、逆用以及角的变换的常用方法.
核 心 素 养
1.借助公式的推导过程,培养数学运算素养.
2. 通过公式的灵活运用,提升逻辑推理素养.
... ... ...
三角恒等变换PPT,第二部分内容:自主预习探新知
新知初探
1.两角和与差的余弦公式
名称 简记符号 公式 使用条件
两角差的余弦公式C(α-β) cos(α-β)=______ α,β∈R
两角和的余弦公式C(α+β) cos(α+β)=______ α,β∈R
2.两角和与差的正弦公式
3.重要结论-辅助角公式
y=asin x+bcos x=_________sin(x+θ)(a,b不同时为0),其中cos θ=________,sin θ=___________.
初试身手
1.cos 57°cos 3°-sin 57°sin 3°的值为( )
A.0 B.12
C.32 D.cos 54°
2.sin 245°sin 125°+sin 155°sin 35°的值是( )
A.-32
B.-12
C.12
D.32
3.若cos α=-35,α是第三象限的角,则sinα-π4=______.
... ... ...
三角恒等变换PPT,第三部分内容:合作探究提素养
给角求值问题
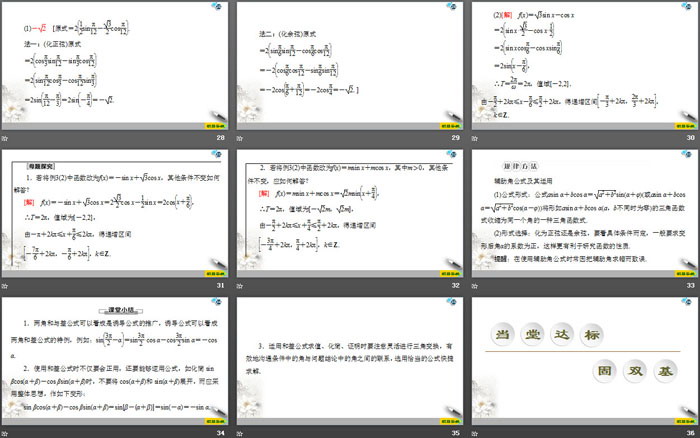
【例1】(1)cos 70°sin 50°-cos 200°sin 40°的值为( )
A.-32 B.-12 C.12 D.32
(2)若θ是第二象限角且sin θ=513,则cos(θ+60°)=________.
(3)求值:(tan 10°-3)cos 10°sin 50°.
规律方法
解决给角求值问题的策略
(1)对于非特殊角的三角函数式求值问题,一定要本着先整体后局部的基本原则,如果整体符合三角公式的形式,则整体变形,否则进行各局部的变形.
(2)一般途径有将非特殊角化为特殊角的和或差的形式,化为正负相消的项并消项求值,化分子、分母形式进行约分,解题时要逆用或变用公式.
提醒:在逆用两角的和与差的正弦和余弦公式时,首先要注意结构是否符合公式特点,其次注意角是否满足要求.
跟踪训练
1.化简求值:
(1)sin 50°-sin 20°cos 30°cos 20°;
(2)sin(θ+75°)+cos(θ+45°)-3cos(θ+15°).
给值求值、求角问题
【例2】(1)已知P,Q是圆心在坐标原点O的单位圆上的两点,且分别位于第一象限和第四象限,点P的横坐标为45,点Q的横坐标为513,则cos∠POQ=________.
(2)已知cos α=55,sin(α-β)=1010,且α,β∈0,π2.求:①cos(2α-β)的值;②β的值.
[思路点拨] (1)先由任意角三角函数的定义求∠xOP和∠xOQ的正弦、余弦值,再依据∠POQ=∠xOP+∠xOQ及两角和的余弦公式求值.
(2)先求sin α,cos(α-β),依据2α-β=α+(α-β)求cos(2α-β).依据β=α-(α-β)求cos β再求β.
规律方法
给值求值问题的解题策略
在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角,具体做法是:
1当条件中有两角时,一般把“所求角”表示为已知两角的和或差.
2当已知角有一个时,可利用诱导公式把所求角转化为已知角.
课堂小结
1.两角和与差公式可以看成是诱导公式的推广,诱导公式可以看成两角和差公式的特例,例如:sin3π2-α=sin3π2•cos α-cos3π2sin α=-cos α.
2.使用和差公式时不仅要会正用,还要能够逆用公式,如化简sin βcos(α+β)-cos βsin(α+β)时,不要将cos(α+β)和sin(α+β)展开,而应采用整体思想,作如下变形:
sin βcos(α+β)-cos βsin(α+β)=sin[β-(α+β)]=sin(-α)=-sin α.
3.运用和差公式求值、化简、证明时要注意灵活进行三角变换,有效地沟通条件中的角与问题结论中的角之间的联系,选用恰当的公式快捷求解.
... ... ...
三角恒等变换PPT,第四部分内容:当堂达标固双基
1.思考辨析
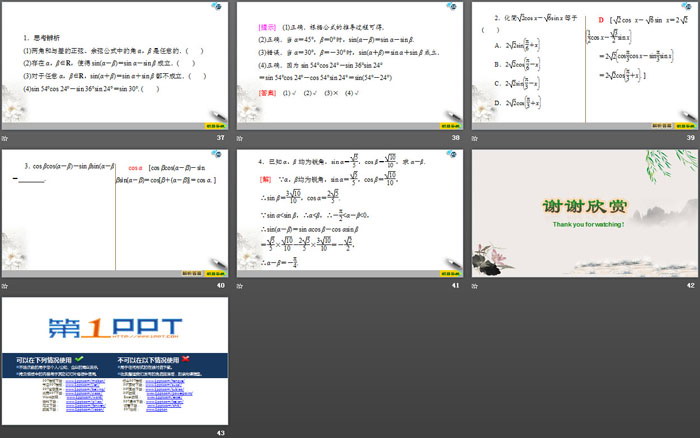
(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( )
(2)存在α,β∈R,使得sin(α-β)=sin α-sin β成立.( )
(3)对于任意α,β∈R,sin(α+β)=sin α+sin β都不成立.( )
(4)sin 54°cos 24°-sin 36°sin 24°=sin 30°.( )
[提示] (1)正确.根据公式的推导过程可得.
(2)正确.当α=45°,β=0°时,sin(α-β)=sin α-sin β.
(3)错误.当α=30°,β=-30°时,sin(α+β)=sin α+sin β成立.
(4)正确.因为sin 54°cos 24°-sin 36°sin 24°
=sin 54°cos 24°-cos 54°sin 24°=sin(54°-24°)
2.化简2cos x-6sin x等于( )
A.22sinπ6+x
B.22cosπ6-x
C.22sinπ3-x
D.22cosπ3+x
3.cos βcos(α-β)-sin βsin(α-β)=________.
4.已知α,β均为锐角,sin α=55,cos β=1010,求α-β.
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,三角恒等变换PPT下载,三角函数PPT下载,两角和与差的正弦余弦公式PPT下载,.PPT格式;
更多关于《 三角函数 三角恒等变换 两角和与差的正弦余弦公式 》PPT课件, 请点击 三角函数PPT三角恒等变换PPT两角和与差的正弦余弦公式PPT标签。
《三角恒等变换》三角函数PPT课件(第5课时简单的三角恒等变换):
《三角恒等变换》三角函数PPT课件(第5课时简单的三角恒等变换) 第一部分内容:学 习 目 标 1.能用二倍角公式导出半角公式,能用两角和与差的三角函数公式导出积化和差、和差化积公式..
《三角恒等变换》三角函数PPT课件(第4课时二倍角的正弦、余弦、正切公式):
《三角恒等变换》三角函数PPT课件(第4课时二倍角的正弦、余弦、正切公式) 第一部分内容:学 习 目 标 1.能利用两角和的正、余弦、正切公式推导出二倍角的正弦、余弦、正切公式(重点) ..
《三角恒等变换》三角函数PPT课件(第3课时两角和与差的正弦、余弦、正切公式):
《三角恒等变换》三角函数PPT课件(第3课时两角和与差的正弦、余弦、正切公式) 第一部分内容:学 习 目 标 1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式. 2.能利用..