
《三角函数的应用》三角函数PPT课件
第一部分内容:学习目标
了解三角函数是描述周期变化现象的重要函数模型
会用三角函数模型解决简单的实际问题
... ... ...
三角函数的应用PPT,第二部分内容:自主学习
问题导学
预习教材P242-P248,并思考以下问题:
1.在简谐运动中,y=Asin(ωx+φ)的初相、振幅、周期分别为多少?
2.解三角函数应用题有哪四步?
新知初探
1.函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
■名师点拨
当A<0或ω<0时,应先用诱导公式将x的系数或三角函数符号前的数化为正数,再确定初相φ.如函数y=-sin2x-π4的初相不是φ=-π4.
2.三角函数模型的建立程序
自我检测
判断正误(正确的打“√”,错误的打“×”)
(1)函数y=Asin(ωx+φ),x∈R的最大值为A.( )
(2)函数y=Asin(ωx-φ)的初相为φ.( )
(3)“五点法”作函数y=2sinx+π3在一个周期上的简图时,第一个点为π3,0.( )
函数y=2sinx2+π5的周期、振幅依次是( )
A.4π,-2 B.4π,2
C.π,2 D.π,-2
函数y=Asin(ωx+φ)+k的图象如图,则它的振幅A与最小正周期T分别是( )
A.A=3,T=5π6 B.A=3,T=5π3
C.A=32,T=5π6 D.A=32,T=5π3
已知某人的血压满足函数解析式f(t)=24sin(160πt)+115.其中f(t)为血压(单位:mmHg),t为时间(单位:min),则此人每分钟心跳的次数(心跳次数即求频率)为( )
A.60 B.70
C.80 D.90
已知电流强度I(A)随时间t(s)变化的关系是I=5sin100πt+π3,则当t=1200s时,电流强度为( )
A.5A B.2.5A
C.2A D.-5A
... ... ...
三角函数的应用PPT,第三部分内容:讲练互动
三角函数在物理中的应用
已知弹簧挂着的小球做上下振动,它离开平衡位置(静止时的位置)的距离h(cm)与时间t(s)的函数关系式为h=3sin2t+π4.
(1)求小球开始振动的位置;
(2)求小球第一次上升到最高点和下降到最低点时的坐标.
求解策略
利用三角函数处理物理学问题的策略
(1)常涉及的物理学问题有单摆,光波,电流,机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
三角函数在实际生活中的应用
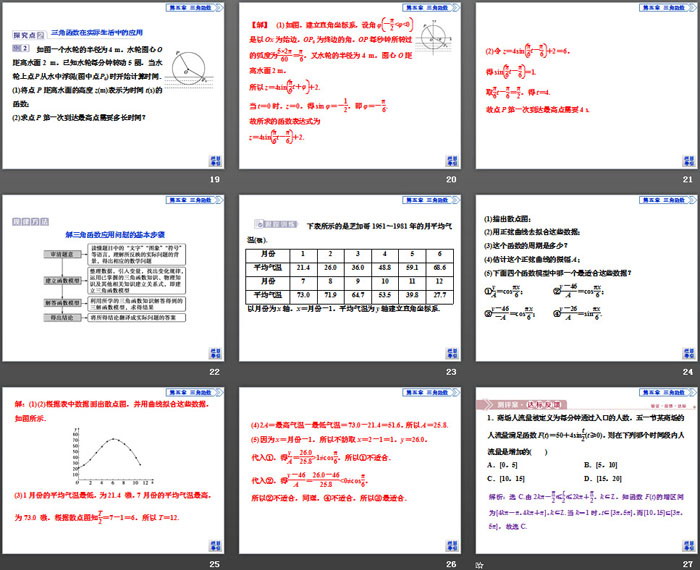
如图一个水轮的半径为4 m,水轮圆心O距离水面2 m,已知水轮每分钟转动5圈,当水轮上点P从水中浮现(图中点P0)时开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)求点P第一次到达最高点需要多长时间?
... ... ...
三角函数的应用PPT,第四部分内容:达标反馈
1.商场人流量被定义为每分钟通过入口的人数,五一节某商场的人流量满足函数F(t)=50+4sint2(t≥0),则在下列哪个时间段内人流量是增加的( )
A.[0,5] B.[5,10]
C.[10,15] D.[15,20]
2.一弹簧振子的位移y与时间t的函数关系式为y=Asin(ωt+φ)(A>0,ω>0),若弹簧振子运动的振幅为3,周期为2π7,初相为π6,则这个函数的解析式为________.
3.某动物种群数量1月1日低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
(1)求出种群数量y关于时间t的函数解析式;(其中t以年初以来经过的月份数为计量单位)
(2)画出种群数量y关于时间t变化的草图.
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,三角函数的应用PPT下载,三角函数PPT下载,.PPT格式;
更多关于《 三角函数的应用 三角函数 》PPT课件, 请点击 三角函数的应用PPT三角函数PPT标签。
《三角函数的应用》直角三角形的边角关系PPT课件:
《三角函数的应用》直角三角形的边角关系PPT课件,共16页。 知识要点基础 知识点1 方向角问题 1.如图,一艘轮船A位于灯塔P的南偏东37方向,且距离灯塔50海里,它沿正北方向航行一段时间..
《三角函数的应用》直角三角形的边角关系PPT(第2课时):
《三角函数的应用》直角三角形的边角关系PPT(第2课时),共24页。 教学目标 1.正确理解方位角、仰角和坡角的概念;(重点) 2.能运用解直角三角形知识解决方位角、仰角和坡角的问题.(..
《三角函数的应用》直角三角形的边角关系PPT(第1课时):
《三角函数的应用》直角三角形的边角关系PPT(第1课时),共18页。 教学目标 1. 理解方位角的概念,能够把实际问题转化为解直角三角形问题,并能适当地选择锐角三角函数关系式加以解决..