

《向量基本定理与向量的坐标》平面向量初步PPT课件(平面向量的坐标及其运算)
第一部分内容:学习目标
了解平面向量的正交分解,掌握向量的坐标表示
理解平面向量坐标的概念,掌握两个向量和、差及数乘向量的坐标运算法则
掌握平面向量的坐标与平面内点的坐标的区别与联系
能根据平面向量的坐标,判断向量是否共线;并掌握三点共线的判断方法
... ... ...
向量基本定理与向量的坐标PPT,第二部分内容:自主学习
问题导学
预习教材P160-P166的内容,思考以下问题:
1.两个向量垂直如何定义?
2.一个向量如何正交分解?
3.向量的坐标定义是什么?
4.如何由a,b的坐标求a+b,a-b,λa的坐标?
5.如何利用向量的坐标运算表示两个向量共线?
... ... ...
向量基本定理与向量的坐标PPT,第三部分内容:新知初探
1.平面向量的坐标
平面上的两个非零向量a与b,如果它们所在的直线互相垂直,我们就称向量a与b______,记作______.规定零向量与任意向量都______.
如果平面向量的基底{e1,e2}中,e1⊥e2,就称这组基底为____________;在正交基底下向量的分解称为向量的____________.
一般地,给定平面内两个相互垂直的单位向量e1,e2,对于平面内的向量a,如果____________,则称(x,y)为向量a的坐标,记作____________.
方便起见,以后谈到平面直角坐标系时,默认已经指定了与x轴及y轴的正方向同向的两个单位向量.此时,如果平面上一点A的坐标为(x,y)(通常记为A(x,y)),那么向量OA→对应的坐标也为(x,y),即OA→=____________;反之结论也成立.
2.平面上向量的运算与坐标的关系
设平面上两个向量a,b满足a=(x1,y1),b=(x2,y2),则
a=b⇔__________________;a+b=__________________.
设u,v是两个实数,那么ua+vb=________________________,ua-vb=____________________.
如果向量a=(x,y),则|a|=_________.
名师点拨
(1)向量的坐标只与起点、终点的相对位置有关,而与它们的具体位置无关.
(2)当向量确定以后,向量的坐标就是唯一确定的,因此向量在平移前后,其坐标不变.
3.平面直角坐标系内两点之间的距离公式与中点坐标公式
设A(x1,y1),B(x2,y2)为平面直角坐标系中的两点,则AB→=__________________;
AB=|AB→|=________________________.
设线段AB中点为M(x,y),则x=___________,y=___________.
4.向量平行的坐标表示
设a=(x1,y1),b=(x2,y2),则a∥b⇔____________.
... ... ...
向量基本定理与向量的坐标PPT,第四部分内容:自我检测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若O为坐标原点,OA→=(2,-1),则点A的坐标为(2,-1).( )
(2)若点A的坐标为(2,-1),则以A为终点的向量的坐标为(2,-1).( )
(3)平面内的一个向量a,其坐标是唯一的.( )
(4)若a=(x1,y1),b=(x2,y2)且b≠0,则x1x2=y1y2.( )
2. 已知向量OA→=(3,-2),OB→=(-5,-1),则向量12AB→的坐标是( )
A.-4,12 B.4,-12
C.(-8,1) D.(8,1)
3. 下列各对向量中,共线的是( )
A.a=(2,3),b=(3,-2) B.a=(2,3),b=(4,-6)
C.a=(2,-1),b=(1,2) D.a=(1,2),b=(2,2)
... ... ...
向量基本定理与向量的坐标PPT,第五部分内容:讲练互动
平面向量的坐标表示
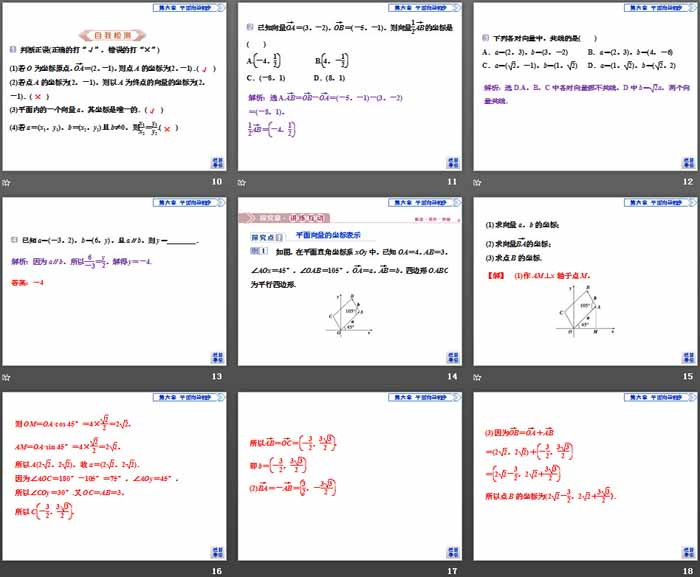
例1 如图,在平面直角坐标系xOy中,已知OA=4,AB=3,∠AOx=45°,∠OAB=105°,OA→=a,AB→=b,四边形OABC为平行四边形.
(1)求向量a,b的坐标;
(2)求向量BA→的坐标;
(3)求点B的坐标.
规律方法
平面内求点、向量坐标的常用方法
(1)求一个点的坐标:可利用已知条件,先求出该点相对应坐标原点的位置向量的坐标,该坐标就等于相应点的坐标.
(2)求一个向量的坐标:首先求出这个向量的始点、终点的坐标,再运用终点坐标减去始点坐标即得该向量的坐标.
平面向量的坐标运算
例2 (1)已知a+b=(1,3),a-b=(5,7),则a=________,b=________.
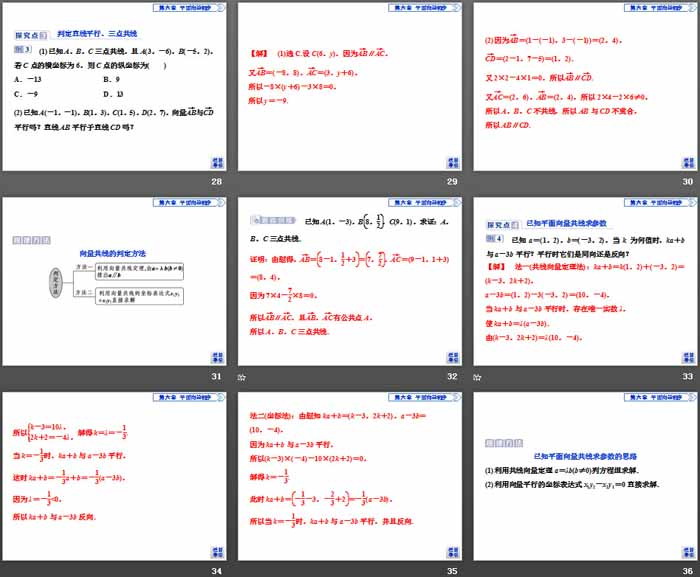
(2)已知A(-2,4),B(3,-1),C(-3,-4),且CM→=3CA→,CN→=2CB→,求M,N及MN→的坐标.
规律方法
平面向量坐标的线性运算的方法
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行.
... ... ...
向量基本定理与向量的坐标PPT,第六部分内容:达标反馈
1.给出下面几种说法:
①相等向量的坐标相同;
②平面上一个向量对应于平面上唯一的坐标;
③一个坐标对应于唯一的一个向量;
④平面上一个点与以原点为始点,该点为终点的向量一一对应.
其中正确说法的个数是( )
A.1 B.2
C.3 D.4
2.下列向量组中,能作为表示它们所在平面内所有向量的一组基底的是( )
A.a=(0,0),b=(2,3)
B.a=(1,-3),b=(2,-6)
C.a=(4,6),b=(6,9)
D.a=(2,3),b=(-4,6)
3.已知两点A(2,-1),B(3,1),则与AB→平行且方向相反的向量a可以是( )
A.(1,-2) B.(9,3)
C.(-2,4) D.(-4,-8)
4.已知平行四边形OABC,其中O为坐标原点,若A(2,1),B(1,3),则点C的坐标为________.
5.已知点A(1,3),B(4,-1),则与向量AB→同方向的单位向量为________.
关键词:高中人教B版数学必修二PPT课件免费下载,向量基本定理与向量的坐标PPT下载,平面向量初步PPT下载,平面向量的坐标及其运算PPT下载,.PPT格式;
更多关于《 平面向量初步 向量基本定理与向量的坐标 平面向量的坐标及其运算 》PPT课件, 请点击 平面向量初步PPT向量基本定理与向量的坐标PPT平面向量的坐标及其运算PPT标签。
《向量基本定理与向量的坐标》平面向量初步PPT课件(向量基本定理 直线上向量的坐标及其运算):
《向量基本定理与向量的坐标》平面向量初步PPT课件(向量基本定理 直线上向量的坐标及其运算) 第一部分内容:学习目标 掌握共线向量基本定理 理解平面向量基本定理 两定理的熟练应用 ..
《向量基本定理与向量的坐标》平面向量初步PPT(平面向量的坐标及其运算):
《向量基本定理与向量的坐标》平面向量初步PPT(平面向量的坐标及其运算) 第一部分内容:课标阐释 1.了解平面向量的正交分解,掌握向量的坐标表示. 2.理解向量坐标的概念,掌握两个向量..
《向量基本定理与向量的坐标》平面向量初步PPT(直线上向量的坐标及其运算):
《向量基本定理与向量的坐标》平面向量初步PPT(直线上向量的坐标及其运算) 第一部分内容:课标阐释 1.理解实数与数轴上的点的一一对应关系及实数运算在数轴上的几何意义. 2.理解向量..